문제
조규현과 백승환은 터렛에 근무하는 직원이다. 하지만 워낙 존재감이 없어서 인구수는 차지하지 않는다. 다음은 조규현과 백승환의 사진이다.

이석원은 조규현과 백승환에게 상대편 마린(류재명)의 위치를 계산하라는 명령을 내렸다. 조규현과 백승환은 각각 자신의 터렛 위치에서 현재 적까지의 거리를 계산했다.
조규현의 좌표 (x1, y1)와 백승환의 좌표 (x2, y2)가 주어지고, 조규현이 계산한 류재명과의 거리 r1과 백승환이 계산한 류재명과의 거리 r2가 주어졌을 때, 류재명이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 이루어져 있다.
한 줄에 x1, y1, r1, x2, y2, r2가 주어진다. x1, y1, x2, y2는 -10,000보다 크거나 같고, 10,000보다 작거나 같은 정수이고, r1, r2는 10,000보다 작거나 같은 자연수이다.
출력
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
해설
이 문제는 테스트 케이스를 통과하더라도, 아래와 같은 이유로 틀리기가 쉽다.
1. 소수점 오차의 문제
2. 모든 케이스를 커버하지 못하는경우
특히 소수점 오차로 인하여 틀리는 경우가 많은 것 같은데, 이 문제는 제곱근을 취하지 않고
비교 대상을 제곱하여 비교연산을 한다면 정수형만으로 문제를 풀 수 있다.
문제를 푸는 핵심은
* 두 점 사이의 거리와 r1, r2를 이용하여 두 원이 어떤 모양으로 접하는지를 파악
x1, y1과 x2,y2가 같은 점인 경우에는
r1, r2의 같다면 무수히 많은 점이 접하게 되고, 다른 경우 하나의 점도 만나지 않게 된다.
이 경우는 간단하기 때문에 그림으로 설명은 생략한다.
점이 다른 경우의 case들을 살펴보면 다음과 같다.
Case1 두 원이 외접하는 경우
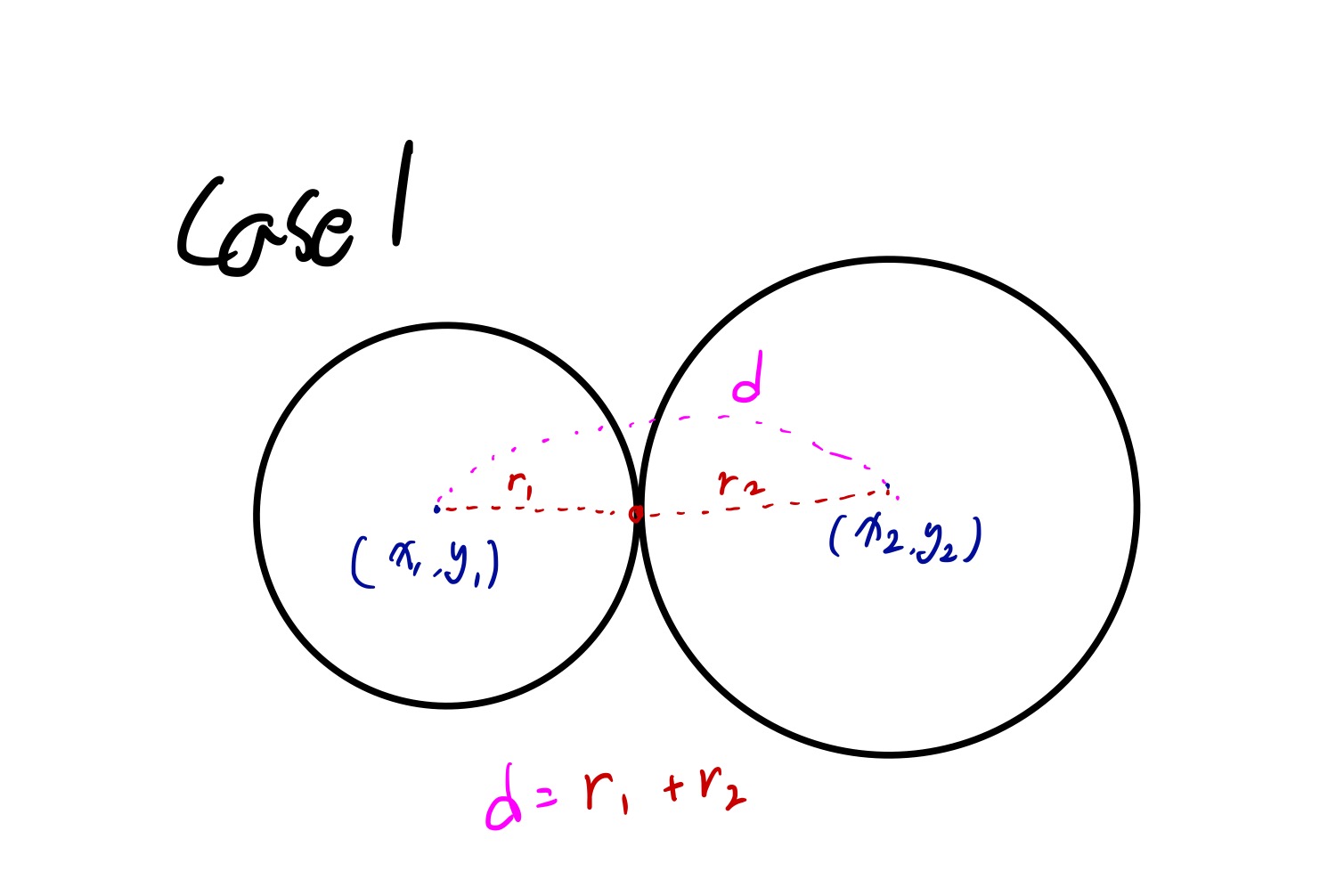
외접하는 경우는 r1 + r1 가 두 점 사이의 거리와 같다.
Case2 두 원이 내접하는 경우

두 원이 내접하는 경우에는 r2-r1의 값이 d와 같다.(단 여기서 r2는 r1, r2 중에 더 긴 값이다.)
하지만 코드상에서는 제곱을 하기때문에 r1, r2 중 누가 더 긴지 비교를 할 필요는 없다.
Case3 두 원이 두 점에서 만나는 경우

이 경우는 Case1과 Case2 사이에서 원이 존재라는 경우를 모두 포함하기 때문에 <, > 를 이용하여 구하면 된다.
Case4 두 원이 만나지 않는 경우

위 Case 들을 고려하여 코드를 작성하면 아래와 같다.
단, 그림에서의 설명과는 다르게 거리의 제곱을 이용하여 비교를 하기 때문에 중간에 **2를 이용하여 제곱한 값을 사용한다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split("\n");
// const input = ['7', '0 0 13 40 0 37', '0 0 3 0 7 4', '1 1 1 1 1 5', '40 0 37 0 0 13', '0 7 4 0 0 3', '1 1 5 1 1 1', '0 0 3000 4000 2500 2500']
const numOfInputs = parseInt(input[0]);
for(let i = 1; i <= numOfInputs; i++) {
const [x1, y1, r1, x2, y2, r2] = input[i].split(" ").map(el => parseInt(el))
const p1 = {x: x1, y: y1}
const p2 = {x: x2, y: y2}
// sqet(root)를 취하는 경우 소수점의 오차 때문에 비교가 힘들기 때문에 제곱된 값을 그대로 사용
const squaredDistance = getSquaredDistance(p1, p2)
console.log(findPointsCount(squaredDistance, r1, r2))
}
function getSquaredDistance(p1, p2) {
return ((p1.x - p2.x) ** 2) + ((p1.y - p2.y) ** 2)
}
function findPointsCount(d, r1, r2) {
const squaredSumR = (r1 + r2) ** 2
const squaredDiffR = (r1 - r2) ** 2
if(d == 0) {
// 원점이 같을 때
if(r1 == r2) return -1
return 0
} else {
if(d > squaredSumR || d < squaredDiffR) {
// Case4 : 0개일때
return 0
} else if(d == squaredDiffR || d == squaredSumR){
// case 1,2: 1개일때(내접 또는 외접)
return 1
} else if(d < squaredSumR){
// case 3: 2개일떄
return 2
}
}
}
|
cs |
'끄적 > Algorithm' 카테고리의 다른 글
| [알고리즘] 백준 - 2447 별 찍기 - 10 해설, node js 구현 (1) | 2021.09.04 |
|---|---|
| [알고리즘] 백준 - 10879 피보나치 수 5 해설 및 node js구현 (0) | 2021.08.31 |
| [알고리즘] 백준 - 3053 택시 기하학 해설, node js 구현 (0) | 2021.08.28 |
| [알고리즘] 백준 - 4153 직각삼각형 node js 구현 (0) | 2021.08.27 |
| [알고리즘] 백준 - 1149 RGB 거리 node js 구현 (0) | 2021.08.22 |
