문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
해설
이 문제는 하오이의 타워 라는 이름으로 유명한 문제이다.
아마 컴퓨터 공학과를 나왔다면, 알고리즘 강의를 듣는 학기초에 한번쯤은 풀어봤을 문제라고 생각한다.
재귀로 풀기 위해서는
function(N)이 function(N-1)로 점점 작아지면서 Base case까지 작아져야한다.
이 문제의 Base Case는 function(1)이 될 것이고, 이 경우 1번에 있는 원판을 3번으로 옮기는 것이 된다.
function(2)인 경우를 생각해보면 아래와 같이 진행이 된다.
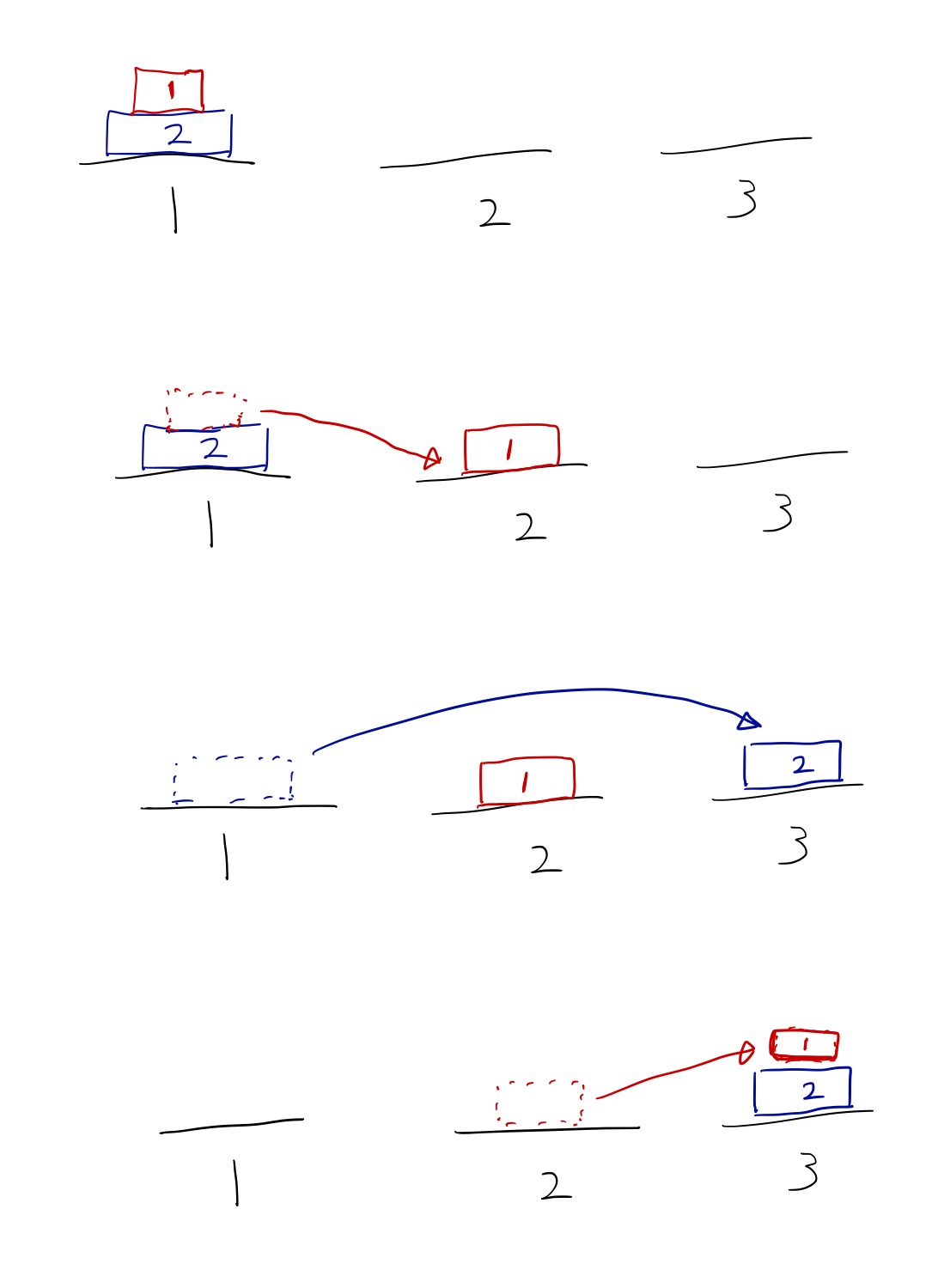
이 문제는 2번 타워를 이용해서 1번에 있는 원판을 3번으로 옮겨라. 라고 표현을 할 수 있다.
function moveVia(N, From, To, Via) 와 같은 함수를 만들어서 풀 수 있다.
그리고 실제로 원판을 옮기는 함수는
function Move(From, To)라는 함수로 정의를 해보자.
위에서 N == 1인 경우에는
Move(1, 3)으로 문제가 풀린다.
N==2인 경우에는
MoveVia(N:2, From:1, To:3, Via:2) 2개의 원판을 1번에서 3번까지 2번 타워를 이용해서 옮겨라
라는 함수를 실행 할 수 있다.
위 그림에서 두번재 단계를 생각해보자
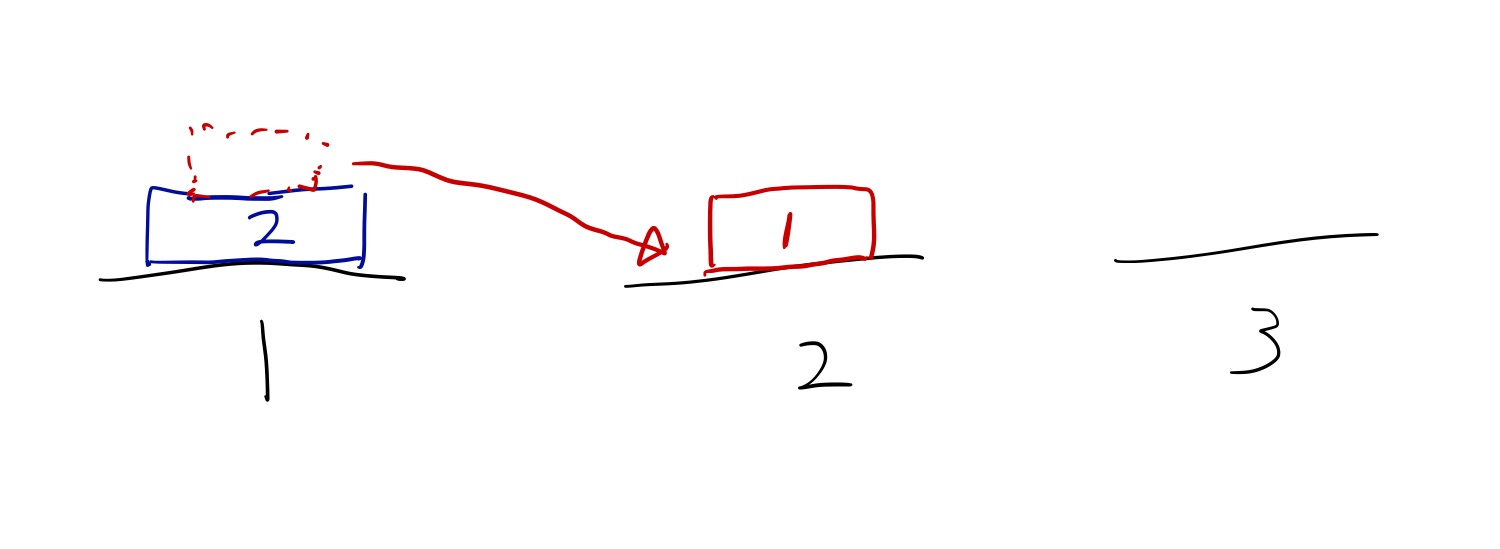
첫번째로는 원판 1개를 From이 아닌 Via에 가져다 놓아야 한다.
왜냐하면, 더 큰 원판이 아래로 가야하기 때문에 작은 원판을 Via에 가져다 놓는 것이다.
즉 MoveVia(N-1, From, Via, To)가 된다. (From에서 Via까지 To를 경유해서 옮겨라.)

그 이후에는 Move(From, To)를 이용하여 실제 우리가 옮기는 원판 중 제일 큰 원판을 To로 옮겨 놓는다.
마지막으로
Via에 있는 1번 원판을 From을 이용하여 3까지 옮기면 되다.

해설에서는 N이 2인 경우만을 생각했지만,
N이 커지더라도 동일한 방법이 적용된다.
달라지는 점은 MoveVia함수가 하나의 원판을 움직이는데서 끝나지 않고,
여러개의 원판을 재귀를 통해서 계속해서 옮기는 작업을 하는 것만 달라진다.
코드로 보면 아래와 같다.
글로 설명하기가 어려워, 다른 분들 블로그를 참고했는데
수학이 싫지 않으신 분은 이분의 블로그를 참고해도 좋을 것 같다.
https://shoark7.github.io/programming/algorithm/tower-of-hanoi
'하노이의 탑' 이해하기
'하노이의 탑' 문제를 이해하고 문제 해결을 위한 핵심 통찰을 살핀 뒤 코드로 작성합니다. 이후 탑의 개수에 따른 총 이동 횟수를 구하는 일반항까지 수학적으로 유도합니다.
shoark7.github.io
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split(' ');
const num = parseInt(input[0]);
var towers = [
[],
[],
[]
]
var moveCount = 0;
var output = []
const hanoi = (num) => {
// init
for(let i = 0; i < num; i++) {
towers[0].push(i)
}
//num개를 0부터 2까지 옮겨라
moveVia(num, 0, 2, 1)
console.log(moveCount)
console.log(output.join('\n'))
}
const move = (from, to) => {
const tmp = towers[from].pop()
towers[to].push(tmp)
moveCount++;
output.push(`${from+1} ${to+1}`)
return;
}
const moveVia = (num, from, to, via) => {
if(num == 1) {
return move(from, to)
}
moveVia(num-1, from, via, to);
move(from, to)
moveVia(num-1, via, to, from)
}
hanoi(num)
|
cs |
'끄적 > Algorithm' 카테고리의 다른 글
| [알고리즘] 백준 - 2231 분해합 해설, node js 구현 (0) | 2021.09.26 |
|---|---|
| [알고리즘] 백준 - 2798 블랙잭 해설, node js 구현 (0) | 2021.09.24 |
| [알고리즘] 백준 - 2447 별 찍기 - 10 해설, node js 구현 (1) | 2021.09.04 |
| [알고리즘] 백준 - 10879 피보나치 수 5 해설 및 node js구현 (0) | 2021.08.31 |
| [알고리즘] 백준 - 1002 터렛 해설, node js 구현 (0) | 2021.08.28 |